Мы привыкли к тому, что стоимость товаров или услуг меняется во времени. Все дорожает. Инфляция. Цены меняются. А вот то, что и деньги могут иметь свою стоимость – эта мысль не всегда очевидна. Сегодня поговорим на важную тему: временная стоимость денег – или то, что нельзя упускать в инвестициях.
Сколько стоят деньги для инвестора
Здесь ничего нового для спецов, но тем, кто начинает – будет полезно
Что нужно знать про деньги? Что цена одной 100 долларовой купюры в 2000, 2020 и 2040 году разная
Технически, это может быть одна и та же купюра, которая 20 лет пролежала у Вас под матрасом, и пролежит там еще столько же. Вы регулярно достаете ее оттуда, смотрите и снова прячете. Ну не знаю, по каким причинам) Не важно. Стоимость 100$будет отличаться во времени из за инфляции
Это важно осознать, чтобы понять в дальнейшем дисконтирование, NPV, расчет денежных потоков и многое другое
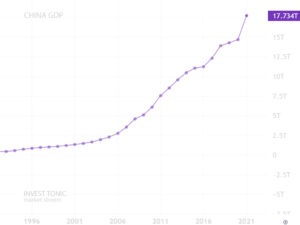
Почему это важно? Посмотрите на Теслу. Денег она не зарабатывает, а инвесторы ее покупают, ожидая, что будущий денежный поток компенсирует переплату в настоящем. Правы ли все эти инвесторы? Я не знаю, но понимая временную стоимость денег, Вы сможете это посчитать со временем сами
Два основных понятия в стоимости денег во времени
Настоящая стоимость: PV (Present Value)
Будущая стоимость: FV (Future Value)
Формула определения будущей стоимости выглядит так:
Зачем вообще формула, спросите Вы. Да любой элементарно посчитает стоимость денег. Например, Вы кладете в банк 500 тысяч рублей под 5% в год с ежегодной капитализацией процентов. Ну что тут сложного, взяли калькулятор, прибавили к 500 тысячам 5% ровно 5 раз, а именно: 500 000 + 5% + 5% + 5% + 5% + 5%
Окей, элементарно. А посчитайте-ка, если Вы положили 500 тысяч на 12 лет с ежемесячной капитализацией процентов на тех же условиях. Что нужно сделать? Годовую доходность (5%) делим на 12, получаем 0.416666 в месяц. И прибавляем к 500 тысячам 0.41666% сколько там, 144 раза??? 12 лет * 12 месяцев = 144 периода. Ну окей, вперед)
И это простая задача. А посчитайте как настоящую справедливую стоимость облигаций в соотношении с ключевой ставкой?
Самое главное, что нужно понять: за любой формулой стоит логика. Если понять эту логику, то формулу легко запомнить и использовать
Итак:
FV – это фьюча вэлью, будущая стоимость. Чтобы ее получить нужно взять настоящую стоимость и умножить на значение в скобках. А что в скобках?
i – это interest rate, т.е. %-я ставка. Это может быть ставка депозита в банке или уровень инфляции
n – это количество периодов. Т.е. если Вам нужно рассчитать % за 5 лет, то это будет 5 периодов. Если капитализация 2 раза в год, то это 10 периодов (5 лет умножить на 2)
Цифра 1 – это просто маркер, показывающий, что Вы со временем увеличиваете (приращиваете) стоимость, так как прибавляете % ставку к числу большее чем 1
В нашем примере про 500 тысяч и 12 лет с ежемесячной капитализацией
FV (будущая стоимость) = PV (500 000) * (1 + 0.004166) в степени 144
Стоп, откуда взялась цифра 0.004166 в скобках. У нас же ежемесячный % был 0.4166%. Это частая ошибка. В скобках у нас десятичные значения. Т.е. 100% это «1». А 10% – это «0.1». Следовательно 1% это «0.01». Таким образом, чтобы перевести 0.4166% в эту систему записи, нужно просто добавить пару нолей после точки. Т.е. 0.41% = 0.0041. Если всем понятно, идем дальше. Кто запутался – гуглим про проценты)
Как понять степень (n) на простом примере
Кладете в банк 1000 рублей под 5% годовых на 3 года
FV = 1000 + 5% + 5% + 5% (народный калькуляторный метод)
По формуле за 3 года это:
FV = 1000 * (1+0.05)3
Если разложить эту формулу по годам, что мы увидим:
FV (год 1) = 1000 * (1+0.05) в степени 1 //Первая степень здесь, так как период один, т.е. один год
+ FV (год 2) = 1000 * (1+0.05) в степени 1
+ FV (год 3) = 1000 * (1+0.05) в степени 1
= FV= 1000 * (1+0.05) в степени 3
По сути, считая доходность за 1 год мы что делаем
Умножаем то, что положили в банк (1000) на (1+0.05), т.е. 1.05 (1 – это 100%, а 1.05 – это 105%). То есть внутри скобок находится значение в 105 % (вложенное + годовой процент)
А степень – это 3 года (количество периодов). Вся простота этой формулы теперь очевидна. И Вы еще много раз ее встретите в качестве составной части более сложных формул
Выводы
Инвестору важно знать концепцию стоимости денег. Это может оценить эффективность инвестиций. Важно понимать доходность портфеля не только в абсолютных величинах. Но и понимать, какие эффективные результаты инвестиций. Т.е. с поправкой на инфляцию и покупательную способность денег в целом.